2023.05.24

N個の商品の中にK個正解がありランダムにM個選ぶ時に正解する個数の期待値

N個の商品の中にK個正解がありランダムでM個選ぶ時に正解する個数の期待値を計算したい。どのように計算すればよいのだろうか。

まず期待値について

確率変数とは

スコアのことを確率変数という。コインを投げて裏が0点、表が1点とした時の、0点とか1点とかのこと。

期待値の計算

この確率変数をそれぞれの点が出る確率と掛け合わせて足すとでる。

公式だと

\begin{aligned} 確率変数　&=> (x_1,x_2,x_3,...x_n) \\ それぞれの変数が出る確率 &=>(p_1,p_2,p_3,...p_n) \end{aligned}

これをそれぞれかけて足す。

\begin{aligned} \\ E(X) = &x_1 p_1 + x_2 p_2 + x_3 p_3 + ... + x_n p_n \\ = &\sum_{n}^{k} { x_k p_k } \end{aligned}

例題

コインを投げた時に表を1点、裏が出たら0点とする。コインを1回投げた時の期待値はいくつか？裏表なのでそれぞれ出る確率は $\dfrac{1}{2}$ なので

\begin{aligned} 確率変数　&=> (0点,1点) \\ それぞれの変数が出る確率 &=>(\dfrac{1}{2},\dfrac{1}{2}) \end{aligned}

なのでそれぞれ掛けて足す

\begin{aligned} E(X) &= (0 \times \dfrac{1}{2}) + (1 \times \dfrac{1}{2}) \\ &= \dfrac{1}{2} \end{aligned}

という当たり前な感じだけど期待値は $\dfrac{1}{2}$ となる

組み合わせについて

まずN個の中からM個選ぶパターンは何個あるかを求めたい。

階乗

n!は1からnまでの全てのせいの整数の積を意味する。

4! = 4 \times 3 \times 2 \times 1

4個のものを選んだ時の組み合わせの数を出したいときに使う。ここら辺は他のサイト参照してくれ。

そして 5個から2個選んだ時のパターンは

5 \times 4

である。何も考えないで普通にこれを出せるが、これを求める式をみてみると、

\begin{aligned} &\dfrac {5 \times 4 \times 3 \times 2 \times 1} {3 \times 2 \times 1} \\ =& \dfrac {5!} {3!} \\ =& \dfrac {5!} {(5-2)!} \end{aligned}

一般解にすると n個からm個選んだ時のパターン数は

\dfrac {n!} {(n-m)!}

順列が関係ないことを考慮する

つまり、アイテムAとアイテムBを選ぶことと、アイテムBとアイテムAを選ぶことは同じとみなしたいので、順序付きの選び方の数（n個からm個選んだ時のパターン数）をm個のアイテムの並べ替えの数（つまりm!）で割る。

なので

\begin{aligned} &\dfrac {n!} {(n-m)!} \cdot \dfrac {1} {m!} \\ =& \dfrac {n!} {m!(n-m)!} \end{aligned}

これでやっとn個のなかからm個選ぶ組み合わせが求められた。

計算する

N個からM個の選び方は $C(n, m) = \dfrac {n!} {m!(n-m)!}$ で求まる。

特定の1つのアイテムが含まれる選び方は $C(n-1, m-1)$ 通り。なぜなら、その1つを選ぶと決まった時点で、残りは $(n-1)$ 個のアイテムから $(m-1)$ 個選ぶ問題になるから。

したがって、特定の1つのアイテムが選ばれる確率は、全体で割って $\dfrac{C(n-1, m-1)} {C(n, m)}$ となる。

ランダムに選んだ場合、任意のアイテムが選ばれるかどうかは独立しているので、 K個の正解を選ぶときに特定の正解が選ばれる期待値は K個すべてについて足し合わせたものと等しくなる。それぞれの正解が選ばれる確率が等しいので、その期待値は K 個の正解すべてについて同じ。

なので、期待値は $k \cdot \dfrac {C(n-1, m-1)} {C(n, m)}$ となる。

これをPythonで書くと

import math

# n choose k
def C(n, k):
    return math.factorial(n) / (math.factorial(k) * math.factorial(n - k))

def expected_value(N, K, M):
    return K * C(N - 1, M - 1) / C(N, M)

print(expected_value(20, 10, 7))  # N=20, K=10, M=7 の例

20個の商品の中に10個正解があり、ランダムで7個選ぶ時に正解する個数の期待値は 3.5となった。ちょうど半分は正解する感じか。ま、あたりまえか。10/20が正解なのだから。

Kの値とMの値を変えてグラフにした。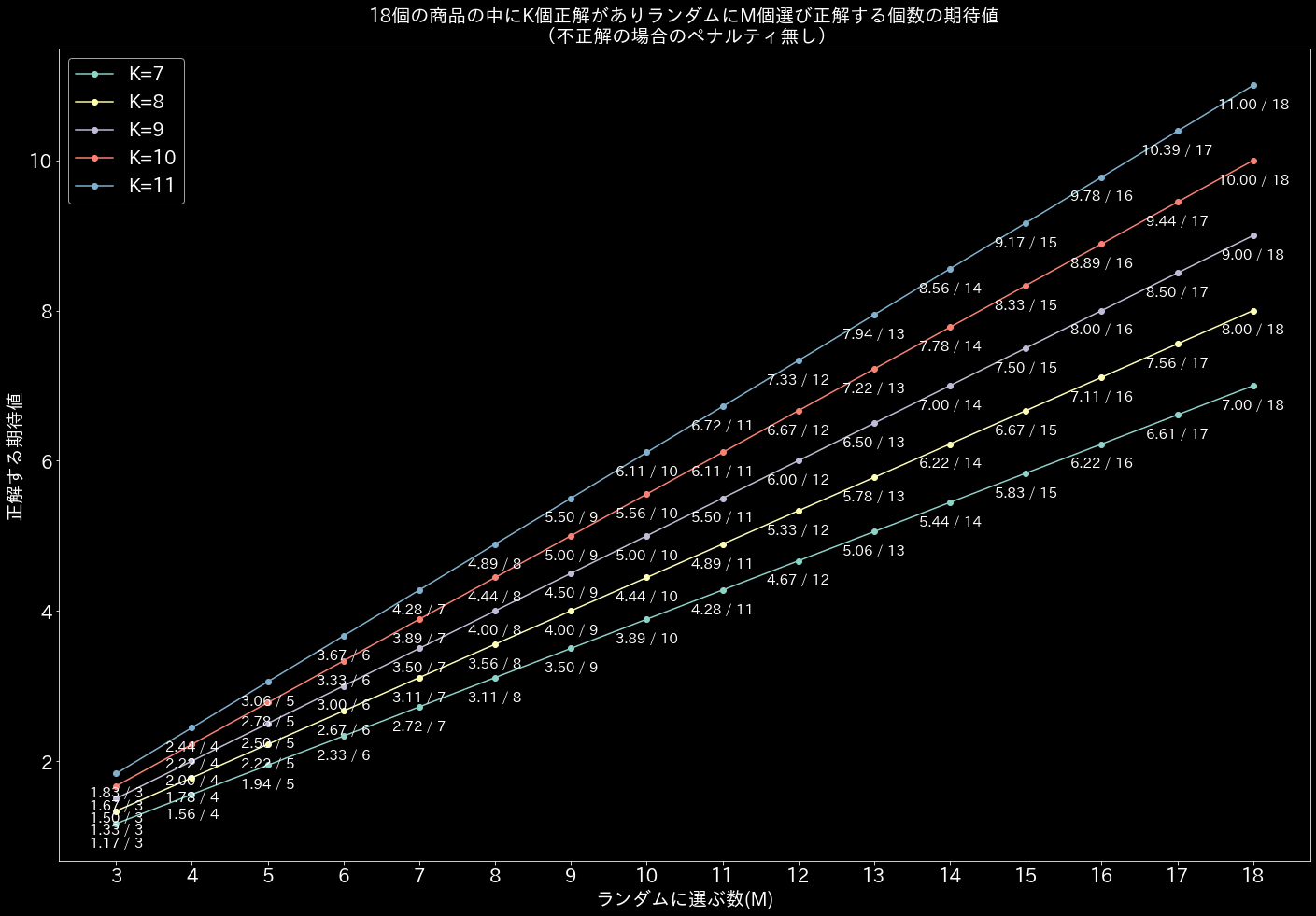たとえば、K=11をみて、11個正解があったときは、18個選べば絶対に11個の正解は含まれているのでこのようなグラフになる。

ここから番外編

不正解の場合の考慮など

てことで色々試す。正解を1点、不正解を-1点とした時の期待値。

一度選ばれた商品が再度選ばれない場合、すなわち無重複の場合の期待値を計算するには、Hypergeometric distribution（超幾何分布）を使います。超幾何分布は、ある母集団から非復元抽出（一度選んだものは元に戻らない抽出）を行ったときの確率分布です。

母集団のサイズをN、成功の数（ここでは正解の数）をK、抽出するサンプルのサイズ（ここでは選ばれる商品の数）をMとすると、超幾何分布の期待値（平均）は次の式で求められます：

E(X) = M * (K / N)

この式は、「サンプル内に見られる成功の期待数は、全体の成功の割合にサンプルの大きさを掛けたものである」という直感的な理解を示しています。つまり、期待値は「成功の割合」に「試行の回数」を掛けたものになります。

したがって、N個の商品の中にK個の正解があり、それらの中からランダムにM個選ぶときの正解の期待値は次のように計算します

def expected_value(N, K, M):
    return M * ((2 * K / N) - 1)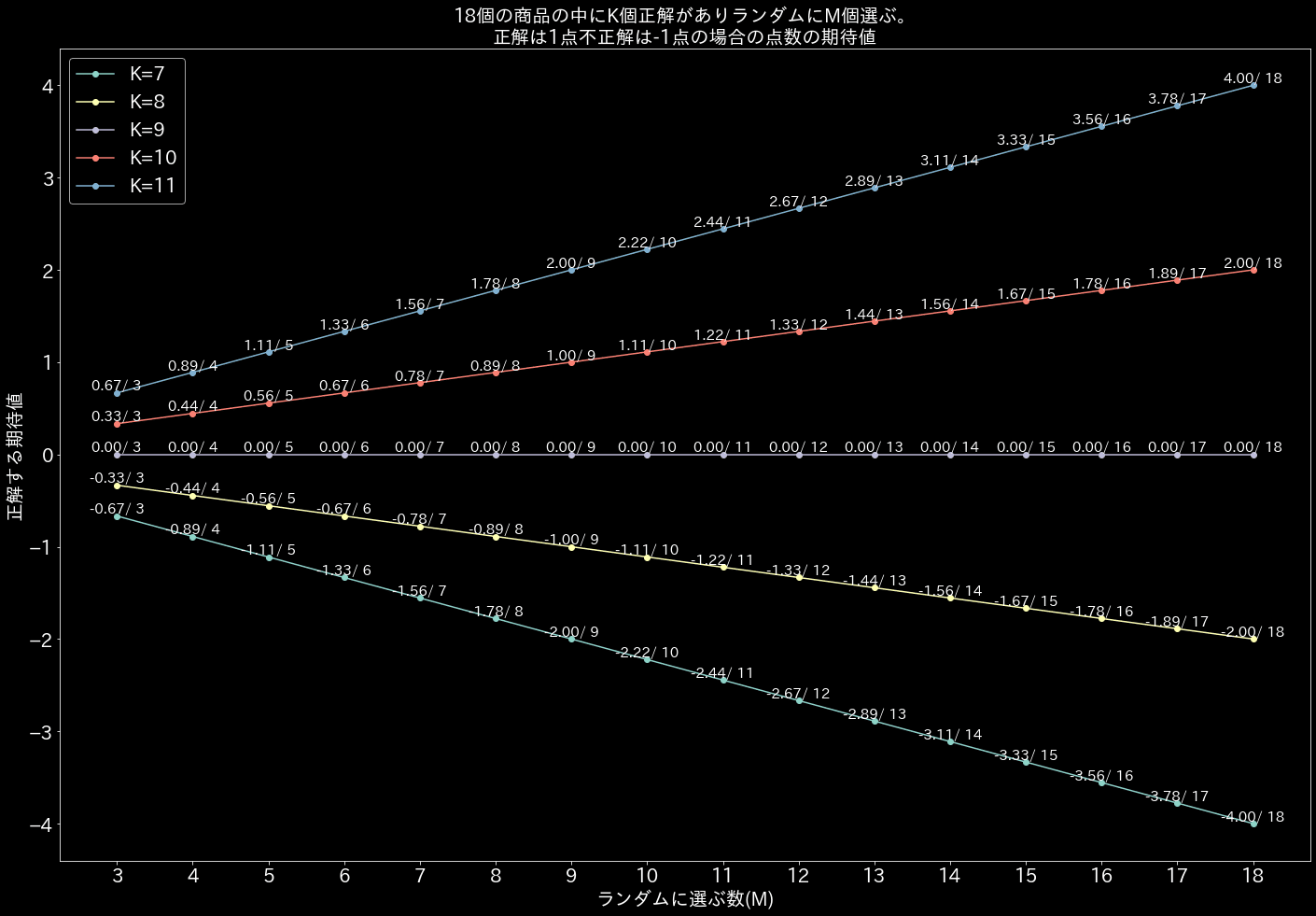

別のパターン。正答率を出す時の分母を、max(正解数, 選択数)で大きい方を使うことにすると、正解数までは選んだ方がお得など。。

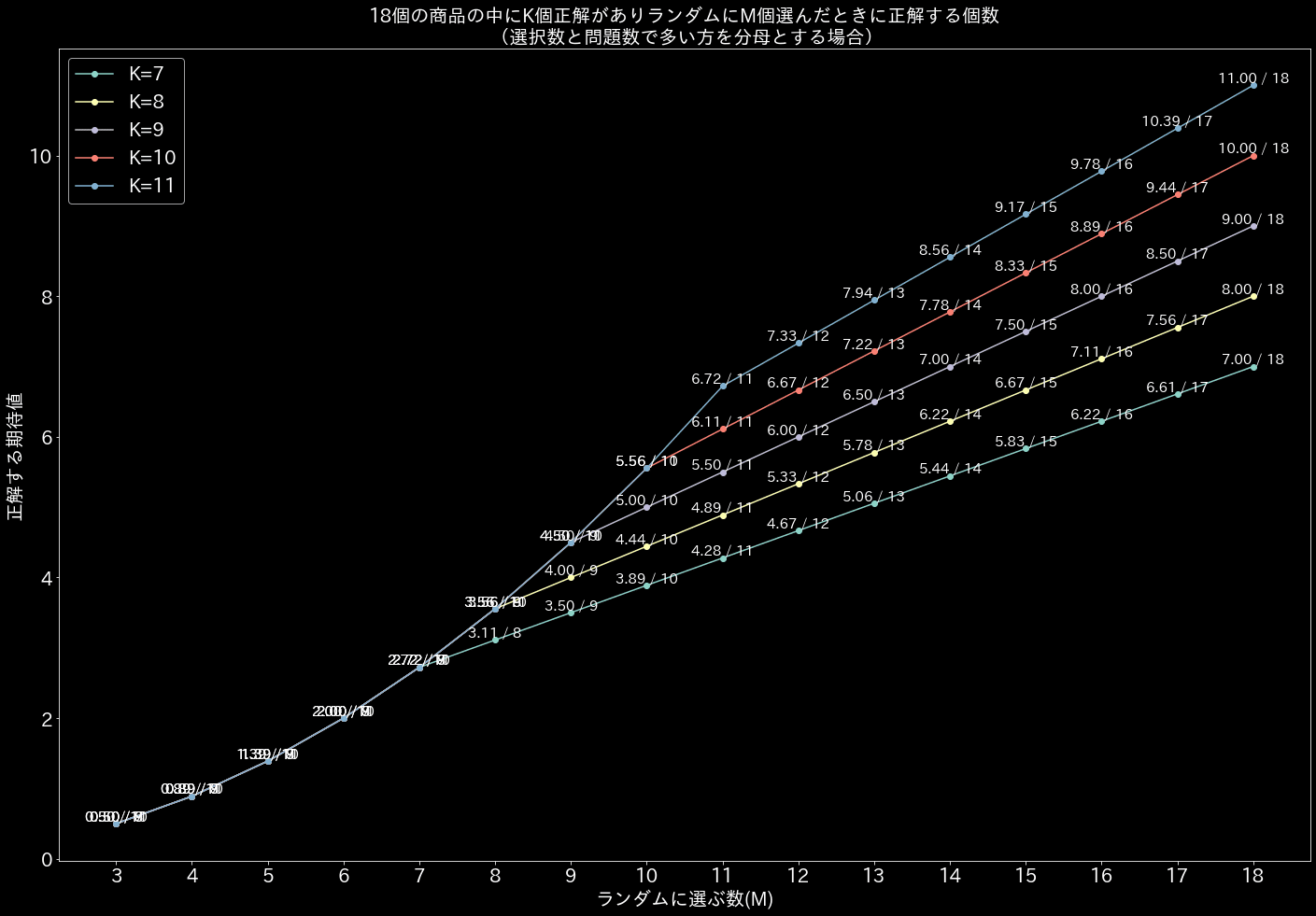
簡単なことだけど数式にすると逆にややこしい説もあるね。。w 以上

VOMIT

N個の商品の中にK個正解がありランダムにM個選ぶ時に正解する個数の期待値

まず期待値について

確率変数とは

期待値の計算

例題

組み合わせについて

階乗

順列が関係ないことを考慮する

計算する

不正解の場合の考慮など

References

N個の商品の中にK個正解があり ランダムにM個選ぶ時に正解する個数の期待値

まず期待値について

確率変数とは

期待値の計算

例題

組み合わせについて

階乗

順列が関係ないことを考慮する

計算する

不正解の場合の考慮など

References

N個の商品の中にK個正解がありランダムにM個選ぶ時に正解する個数の期待値