2022.02.23

投射運動と等加速度運動

KaTex表記の練習として、投射運動の数式を書いていく。角度 $\theta$ で速度uでボールを投げた時の軌跡を出す数式を書いてプログラムにしてグラフにする。

xが水平,yが垂直の座標を表すとして、重力を考えない場合、三角関数で以下のように出せる。

x = u \cdot \cos\theta \\ y = u \cdot \sin\theta

時間をtとすると。

x = u (\cos\theta) \cdot t \\ y = u(\sin\theta) \cdot t

と表せる。それをグラフにすると、

from matplotlib import pyplot as plt
import math

u = 30 # 秒速30m で投げる。
angle = 60 # 60度の角度で投げる。
theta = angle/180 * math.pi # 弧度法に変換

t_range = range(0,6) # 0秒~6秒の間で調べる。

pos_x = []
pos_y = []


for sec in t_range:
    x = u * math.cos(theta) * sec
    y = u * math.sin(theta) * sec
    pos_x.append(x)
    pos_y.append(y)


plt.plot(t_range,pos_y)
plt.xlabel('時間（秒）')
plt.ylabel('Y座標 (メートル)')
plt.title('等速直線運動')
plt.legend(['y'])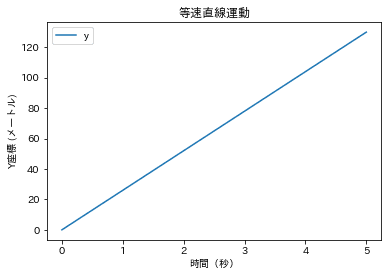

当たり前だがこうなる。

次に垂直方向のy座標は重力の影響を受ける場合を考える。先程のy座標の式から重力加速度分を引けば良い。重力加速分をどうやって表すか。高校文系だった人間には分からないが、物理の等加速度運動の公式に出てくるやつを使えばできる。

等加速度運動の公式

\begin{aligned} ① &v = v_0 + at \\ ② &x = v_0t + \frac{1}{2} at^2 \\ ③ &v^2 - v_0^2 = 2ax \end{aligned}

a : 加速度[m/s^2]
t : 時間[s]
x : 変位[m]
$v_0$ : 初速度 [m/s]
$v$ : 加速後の速度[m/2]

① $v = v_0 + at$

これは $v_0$ が初速度でそれに、速さ(a)と時間(t)の積を足したものが速度ということなので、直感でもわかる。

もう少し詳しく書くと、中学くらいで習った傾きの公式が

a = \frac{ y_2 - y_1 } { x_2 - x_1}

で、A : (2, 4), B : (4, 8) だとしたらこの傾きは

\begin{aligned} a &= \frac{ 4 - 2 } { 8 - 4} \\ a &= \frac{1}{2} \end{aligned}

なので、傾きが $\frac{1}{2}$ になる。これと考え方一緒で、
速度から初速度を引き、それを時間で割ることで単位時間の加速度がだせる。

a = \frac{v - v_0} {t}

（ちなみにこれが加速度の公式らしい。）これを移行して変形させると

\begin{aligned} a &= \frac{v - v_0} { t } \\ a \cdot t &= \frac{v - v_0} { \bcancel{t} } \cdot \bcancel{t} \\ at &= v - v_0 \\ v & = v_0 + at \end{aligned}

となって、①の式が出来る。

② $x = v_0t + \frac{1}{2} at^2$

これが本題。等加速している物体の、時間Tの位置をどう求めるか。

まず、直線運動する物体の位置を求める。
位置( $x$ ) = 速度（ $v_0$ ） $\times$ 時間( $t$ )なので

x = v_0 \cdot t

これは小学生で習った。では加速度運動の位置は？切片が初速度の速度の方程式の面積を出してあげれば良い。

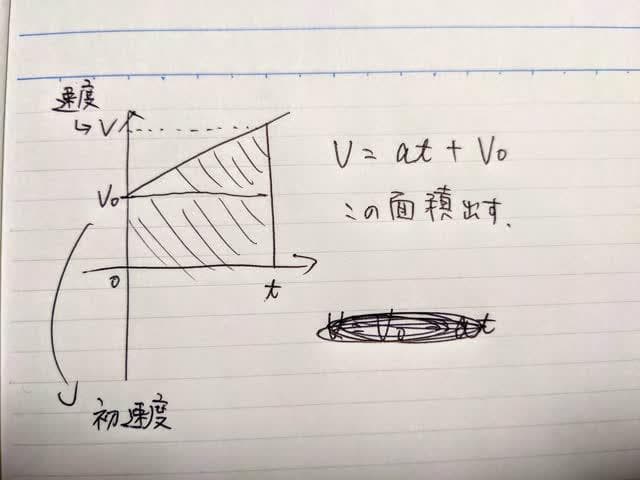台形の面積の計算

\begin{aligned} S =& \{(at + v_0) + (v_0)\} \cdot t \cdot \frac{1}{2} \\ =& (at + 2v_0) \cdot t \cdot \frac{1}{2} \\ =&　v_0t + \frac{1}{2}at^2 \end{aligned}

等加速度運動の公式の②の式が導かれた。（今回は等加速度方程式の③は使わないので無視。）そして $x = v_0t + \frac{1}{2} at^2$ に　初速度0,加速度をgにして重力加速度を入れてみると。

x = \frac{1}{2}gt^2

となった。これはつまりものをそのまま落とした時の方程式。
これを最初にグラフにした等速直線運動のy座標から引いてやる。

y = u (\sin\theta) \cdot t - \frac{1}{2}gt^2

で計算できる。

from matplotlib import pyplot as plt
import math

u = 30 # 秒速30m で投げる。
angle = 60 # 60度の角度で投げる。
theta = angle/180 * math.pi # radianに返還
g = 9.8 # 重力加速度

range_end = u * math.sin(theta) / g * 2 # 頂点に到達する時間の2倍でボールが地面に落ちるまでの時間を計算

print('ボールが地上に落ちてくる時間 : {0}'.format(range_end))

# range_end = 3

def frange(start,end,inc):
    numbers = []
    while start < end:
        numbers.append(start)
        start += inc

    return numbers

t_range = frange(0,range_end, 0.1) # 0秒~ボールが落ちるまで

pos_x = []
pos_y = []


for sec in t_range:
    x = u * math.cos(theta) * sec
    y = u * math.sin(theta) *sec - (1/2 * g * sec*sec)
    pos_x.append(x)
    pos_y.append(y)

plt.plot(t_range,pos_y)
plt.xlabel('時間（秒）')
plt.ylabel('Y座標 (メートル)')
plt.title('投射運動')
plt.legend(['y'])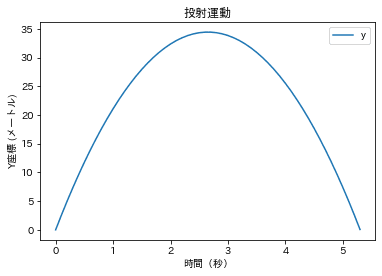

これで、無事に投射運動のグラフが書けたが、上の式でボールが落ちてくるまでの時間を計算して範囲を指定してplotしてしまっている。このボールが落ちてくる時間をどうやって計算しているかというと、

y = u(\sin\theta)\cdot t - \frac{1}{2}gt^2

をtについて微分して

y'= u(\sin\theta) - \frac{ \bcancel{2}} {\bcancel{2}} gt \\ y'= u(\sin\theta) - gt

これをグラフにすると

from matplotlib import pyplot as plt
import math

u = 30
theta = math.radians(60)
g = 9.8

trange = frange(0,5,0.1)

pos_y = []
for t in trange:
    y = u * math.sin(theta) - g * t
    pos_y.append(y)


plt.plot(trange, pos_y)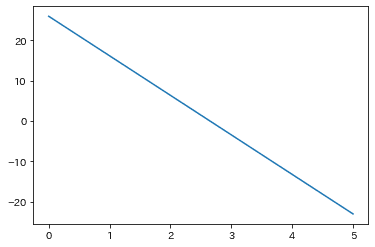

$y = 0$ の時が分岐点なので(速度がプラスからマイナスに切り替わる二次関数の頂点)

u(\sin\theta) - gt = 0

のときに重力加速度とボールの速度を入力すると、時間がもとまる。移行すると

t = \frac{ u \cdot \sin\theta } { g }

で代入 [ボールの速度 : 30 m/sec, 角度 : 60度, 重力加速度 : 9.8 m/sec] $\sin60 = print(math.sin(theta)) = 0.8660254037844386$ として

\begin{aligned} t &= \frac{ 30 \cdot \sin60 } { 9.8 } \\\\ &= \frac{ 30 \cdot 0.8660254037844386 } { 9.8 } \\\\ &= 2.651098174850322秒 \end{aligned}

これがy= 0の時の秒数でこれを2倍すると落下時の時間がわかる。 5.302196349700644秒これをplotするときに範囲として使っている。

今回はここまで。

投射運動と等加速度運動

等加速度運動の公式

① v=v0+atv = v_0 + atv=v0​+at

② x=v0t+12at2x = v_0t + \frac{1}{2} at^2x=v0​t+21​at2

① $v = v_0 + at$

② $x = v_0t + \frac{1}{2} at^2$